# 这里相当于投了15次硬币
rbinom(n = 15, prob = 0.5, size = 1) [1] 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0随机变量分为离散型随机变量和连续性随机变量两种。这里仅讨论离散型随机变量，他们的定义，例子和在R里怎么调用。
1 伯努利分布
伯努利随机变量是最简单的了，就是投掷一枚硬币，是正面朝上还是反面朝上。比如记正面朝上为1，反面朝上为0。
在R里，生成伯努旅随机变量的函数如下：
查看rbionm函数的帮助，帮助里有4个函数：
dbinom：概率密度函数
pbinom：概率质量函数
qbinom：分位函数
rbinom：随机变量生成函数（上面见过了）
dbinom(0:1, size = 1, prob = 0.5)[1] 0.5 0.5就是取0，1的概率都是0.5。
pbinom(0:1, size = 1, prob = 0.5)[1] 0.5 1.0取小于等于0的概率是0.5，小于等于1的概率是1。
qbinom(c(0.5, 1), size = 1, prob = 0.5)[1] 0 1相当于pbionm的逆函数了，提供概率质量函数的概率，给出对应概率的取值。
其他函数也有这4个函数组合，同样的前缀。类似的用法，只是需要提供对应分布的参数。
2 二项分布
二项分布是伯努利分布的扩展，伯努旅分布是投掷1次硬币，二项分布是投掷多次硬币，看正面朝上的次数。
# 每一个值表示投掷10次硬币，有多少次正面朝上。有20个值时这个实验重复了20次
rbinom(20, size = 10, prob = 0.5) [1] 4 3 6 6 6 3 5 4 7 6 3 7 5 3 6 6 4 8 4 4dbinom(0:10, size = 10, prob = 0.5) [1] 0.0009765625 0.0097656250 0.0439453125 0.1171875000 0.2050781250
[6] 0.2460937500 0.2050781250 0.1171875000 0.0439453125 0.0097656250
[11] 0.0009765625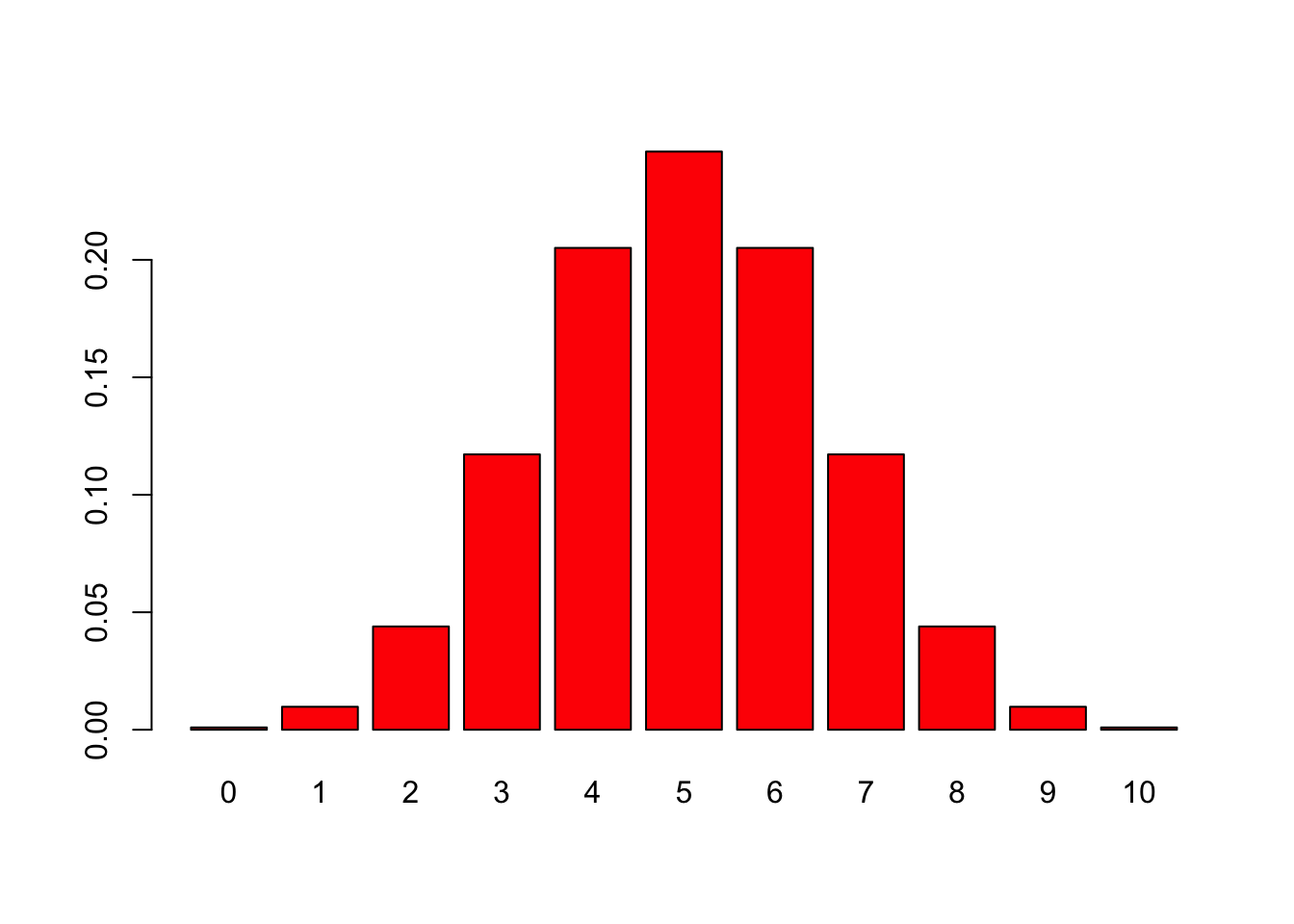barplot(dbinom(0:10, size = 10, prob = 0.5), names.arg = 0:10, col = "red")
果然5次正面朝上的概率是最高的。
3 多项分布
多项分布是二项分布的扩展，二项分布是重复伯努利实验，伯努利实验每次只有2个结果。多项分布相当于伯努利实验每次有多个结果。
比如每次投掷一个6面的骰子🎲，重复10次，统计1：6出现次数的分布就是服从多项分布的。
pvec = rep(1/6, 6)
rmultinom(5, size = 10, prob = pvec) [,1] [,2] [,3] [,4] [,5]
[1,] 3 1 2 1 0
[2,] 2 2 0 0 1
[3,] 0 1 5 4 4
[4,] 2 1 1 1 2
[5,] 2 4 0 1 1
[6,] 1 1 2 3 2每一列是一次实验（投掷10次骰子）的结果统计
dmultinom(c(2, 2, 2, 2, 2, 0), size = 10, prob = pvec)[1] 0.0018754294 泊松分布
我开始认识泊松分布是的时候是它的公式，有点晕，不知所云。后来知道泊松分布其实就是特殊情况下的二项分布的近似，泊松分布的公式也是这么推导出来的。我们看看是什么情况。
《Modern Statistics for Modern Biology》里有一个很好的例子。HIV病毒每复制一次，每个碱基突变的概率是0.0005，HIV基因组大约是10000bp，那么HIV复制一次，有多少个碱基发生突变呢？这个就是符合速率为0.0005 x 10000 = 5泊松分布。
rpois(20, 5) [1] 6 3 5 11 5 3 6 5 9 5 3 6 4 5 10 8 7 7 2 6barplot(dpois(0:10, 5), names.arg = 0:10, col = "red")
HIV复制一次，相当于10000个碱基每个复制一次，每个碱基突变的概率是0.0005。相当于投掷10000次硬币，正面朝上的概率是0.0005，最后有多少次正面朝上！
barplot(dbinom(0:10, size = 10000, prob = 0.0005), names.arg = 0:10, col = "red")
上面两个图是一致的，不信，再看看具体概率：
dpois(0:10, 5) [1] 0.006737947 0.033689735 0.084224337 0.140373896 0.175467370 0.175467370
[7] 0.146222808 0.104444863 0.065278039 0.036265577 0.018132789dbinom(0:10, size = 10000, prob = 0.0005) [1] 0.006729527 0.033664467 0.084194850 0.140366868 0.175493694 0.175511252
[7] 0.146259377 0.104460531 0.065274768 0.036252875 0.018119183
Important
当二项分布实验次数n很大，p很小时，可以近似为速率参数为np的泊松分布。
5 负二项分布
我们先看一个例子，有一罐鱼皮花生，其中吃到发霉花生的概率1/10，如果我想吃5个好花生，总共吃的发霉花生个数就是符合负二项分布（其实我不会吃的，会吐掉，然后漱口）。
rnbinom(10, size = 5, prob = 9/10) [1] 2 0 0 0 0 0 1 0 0 0这里我做了10次实验，看来大概率是吃到1-2个发霉花生。
barplot(dnbinom(0:5, size = 5, prob = 9/10), names.arg = 0:5, col = "red")
6 几何分布
几何分布也是二项分布的延伸。还是举花生的例子，吃到发霉发生的概率是1/10，那么我第一次吃到发霉花生时，总共吃了几个好花生，就是符合几何分布的。
rgeom(10, prob = 1/10) [1] 15 24 6 15 16 31 7 1 2 21dgeom(0:3, prob = 1/10)[1] 0.1000 0.0900 0.0810 0.0729吃到0个好花生的概率是0.1，1个好花生的概率是0.9 x 0.1 = 0.09，2个好花生的概率是0.9 x 0.9 x 0.1 = 0.081。
7 超几何分布
超几何分布应该在基因富集分析的应用而鼎鼎有名。
其实大家高中就学过了。有20个球，其中14个是红球，6个是黑球，随机取5个球不放回，取到的红球的数目就是符合超几何分布。
rhyper(0:5, 14, 6, 5)[1] 3 1 3 2 3 3barplot(dhyper(0:5, 14, 6, 5), names.arg = 0:5, col = "red")