import torch
import math
import matplotlib.pyplot as plt
from functools import partial

torch.set_printoptions(precision=3, linewidth=140, sci_mode=False)

1 K-means

This implement of k-means is a home work of fastai course part2.

2 Create Data

n_clusters = 6
n_samples = 250

centroids = torch.rand(n_clusters, 2)*70-35

centroids

tensor([[ -3.628,  18.403],
        [ -7.049,  -8.394],
        [ 14.369,   2.944],
        [ 22.497, -17.995],
        [-24.635,  33.245],
        [ 13.786,  12.422]])

from torch.distributions.multivariate_normal import MultivariateNormal
from torch import tensor

def sample(m): return MultivariateNormal(m, torch.diag(tensor([30.,30.]))).sample((n_samples,))

slices = [sample(c) for c in centroids]
data = torch.cat(slices)
data.shape

torch.Size([1500, 2])

def plot_data(centroids, data, n_samples, ax=None):
    if ax is None: _,ax = plt.subplots()
    for i, centroid in enumerate(centroids):
        samples = data[i*n_samples:(i+1)*n_samples]
        ax.scatter(samples[:,0], samples[:,1], s=1)
        ax.plot(*centroid, markersize=10, marker="x", color='k', mew=5)
        ax.plot(*centroid, markersize=5, marker="x", color='m', mew=2)

plot_data(centroids, data, 250)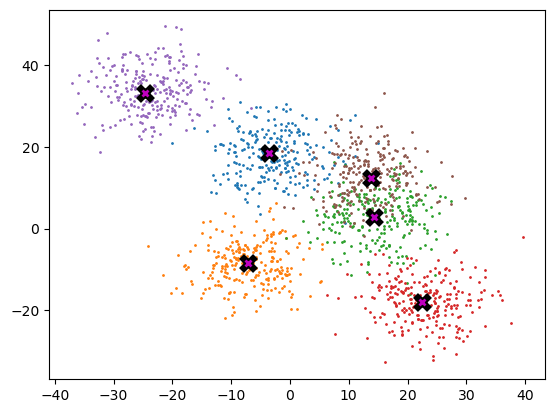

3 k-means

X = data.clone()

3.1 Init mean

k = 6

perm = torch.randperm(X.size(0))

idx = perm[:k]
means = X[idx].clone()
means

tensor([[ 13.227,  -8.303],
        [ 11.784,  11.362],
        [ 15.491,  -4.326],
        [ 12.847, -19.425],
        [ 15.780,  17.934],
        [ -2.511,  -3.635]])

plot_data(means, X, 250)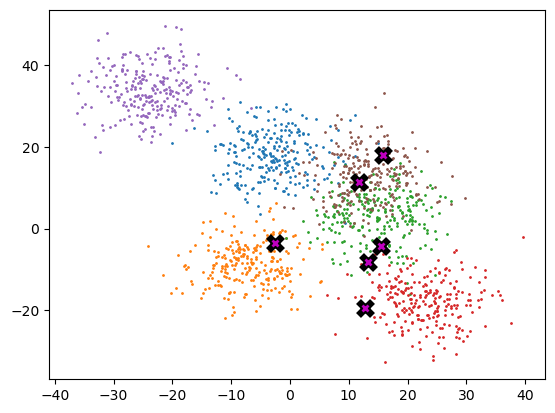

3.2 Calculate distance

means.shape, X.shape

(torch.Size([6, 2]), torch.Size([1500, 2]))

means[:, None].shape, X[None].shape

(torch.Size([6, 1, 2]), torch.Size([1, 1500, 2]))

(means[:, None] - X[None]).shape

torch.Size([6, 1500, 2])

mm = means[:, None] - X[None]

l2 = torch.einsum('ijk, ijk->ij', mm, mm)

l2

tensor([[ 734.640,  709.354,  706.383,  ...,  569.188, 1460.258, 1255.919],
        [ 297.342,  241.198,  183.035,  ...,   60.147,  350.148,  249.417],
        [ 684.036,  643.628,  618.255,  ...,  380.736, 1172.179, 1018.224],
        [1281.019, 1277.346, 1310.853,  ..., 1213.889, 2434.660, 2157.942],
        [ 494.725,  412.703,  316.399,  ...,   17.422,  144.967,  130.433],
        [ 232.653,  253.557,  305.201,  ...,  793.216, 1409.568, 1052.514]])

l2.shape

torch.Size([6, 1500])

(mm * mm).sum(2)

tensor([[ 734.640,  709.354,  706.383,  ...,  569.188, 1460.258, 1255.919],
        [ 297.342,  241.198,  183.035,  ...,   60.147,  350.148,  249.417],
        [ 684.036,  643.628,  618.255,  ...,  380.736, 1172.179, 1018.224],
        [1281.019, 1277.346, 1310.853,  ..., 1213.889, 2434.660, 2157.942],
        [ 494.725,  412.703,  316.399,  ...,   17.422,  144.967,  130.433],
        [ 232.653,  253.557,  305.201,  ...,  793.216, 1409.568, 1052.514]])

(mm * mm).sum(2).shape

torch.Size([6, 1500])

3.3 Select nearest group

group = torch.argmin(l2, dim=0)

group.shape

torch.Size([1500])

3.4 Update mean

X[group == 0].shape

torch.Size([47, 2])

torch.mean(X, 0)

tensor([2.815, 6.901])

for i in range(k):
    means[i] = torch.mean(X[group == i], 0)

means

tensor([[ 15.741, -10.534],
        [  0.595,  16.672],
        [ 18.710,  -2.103],
        [ 22.234, -19.903],
        [  2.595,  25.472],
        [-11.656,   2.780]])

plot_data(means, data, 250)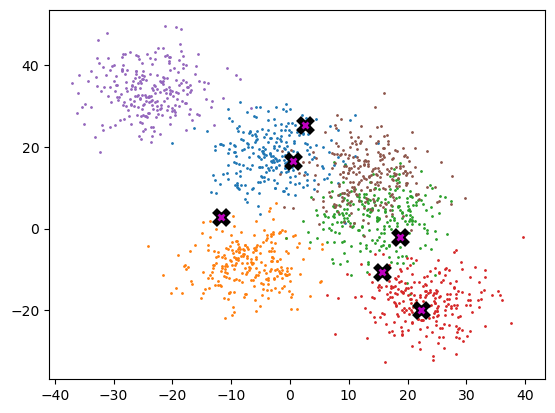

3.5 Write update loop

def update(means, X, n):
    for t in range(n):
        mm = means[:, None] - X[None]
        l2 = torch.einsum('ijk, ijk->ij', mm, mm)
        group = torch.argmin(l2, dim=0)
        for i in range(k):
            means[i] = torch.mean(X[group == i], 0)

update(means, X, 10)

plot_data(means, data, 250)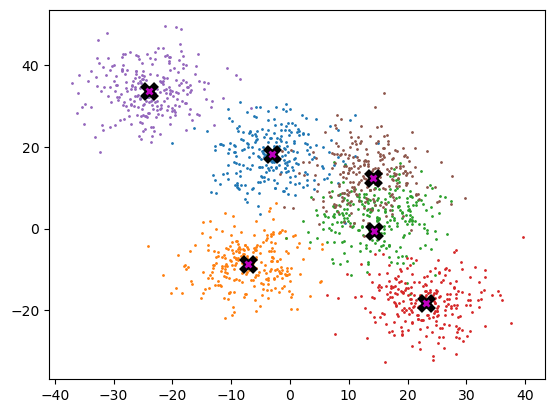

3.6 Write k-means function

def kmeans(X, k, n):
    # init means
    perm = torch.randperm(X.size(0))
    idx = perm[:k]
    means = X[idx].clone()

    for t in range(n):
        mm = means[:, None] - X[None]
        l2 = torch.einsum('ijk, ijk->ij', mm, mm)
        group = torch.argmin(l2, dim=0)
        for i in range(k):
            means[i] = torch.mean(X[group == i], 0)
    
    return means

means = kmeans(X, 6, 10)

plot_data(means, data, 250)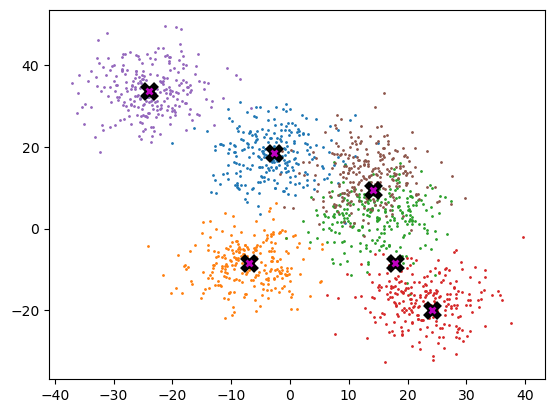

4 Animation

from matplotlib.animation import FuncAnimation
from IPython.display import HTML

def init_means(X, k):
    perm = torch.randperm(X.size(0))
    idx = perm[:k]
    means = X[idx].clone()
    return means

def one_update(X, means, k):
    mm = means[:, None] - X[None]
    l2 = torch.einsum('ijk, ijk->ij', mm, mm)
    group = torch.argmin(l2, dim=0)
    for i in range(k):
        means[i] = torch.mean(X[group == i], 0)
    return group

def plot_data_group(centroids, group, data, ax=None):
    if ax is None: _,ax = plt.subplots()
    for i, centroid in enumerate(centroids):
        samples = data[group == i]
        ax.scatter(samples[:,0], samples[:,1], s=1)
        ax.plot(*centroid, markersize=10, marker="x", color='k', mew=5)
        ax.plot(*centroid, markersize=5, marker="x", color='m', mew=2)

def do_one(d, means, k):
    pre_means = means.clone()
    group = one_update(X, means, k)
    ax.clear()
    plot_data_group(pre_means, group, X, ax=ax)

X = data.clone()
k = 5
fig,ax = plt.subplots()
means = init_means(X, k)
f1 = partial(do_one, means=means, k=k)
ani = FuncAnimation(fig, f1, frames=10, interval=500, repeat=False)
plt.close()
HTML(ani.to_jshtml())